浦东新区八校初中三年级上期中数学联考
（时间：
100分钟，总分：
150分）
1、选择题：（本大题共6题，每题4分，满分24分）
1、已知：在一张比率尺为1：20000的地图上，量得A、B两地的距离是5
，那样A、B两地的实质距离是……
（ ）A）500 B）1000 C）5000 D）10000
2、已知两个相似三角形的相似比为4：9，则它们周长的比为…………………（ ）
A）2：3 B）4：9 C）3：2 D）16：81
3、已知
中，
，CD是AB上的高，则
=………………（ ）
A） B）
C）
D）
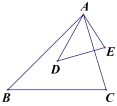4、如图，∠BAC=∠D，要使△ABC与△ADE相似，还需满足下列条件中…………（ ）
（A）
； （B）
；
（C）
； （D）
．
5、在△ABC中，点D、E分别在边AB、AC上，假如AD=2，BD=4，那样由下列条件可以判断DE//BC的是（ ）
（A）
； （B）
； （C）
； （D）
．
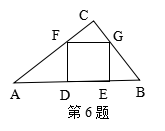6、如图，在RT△ABC中，∠C=90°，BC=3，AC=4，四边形DEGF为内接正方形，那样AD：DE：EB为………………………………………………………………（ ）
（A）3︰4︰5 （B）16︰12︰9 （C）9︰12︰16 （D）16︰9︰25
2、填空题：（本大题共12题，每题4分，满分48分）
7、设
，那样
______________；
8、如图，AB∥CD，AD、BC相交于O，且AO=5，BO=4，CO=16，那样DO=______________；
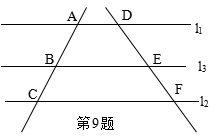
9、如图，直线
∥∥，AB=4， BC=3，DF=14，那样DE=______________；
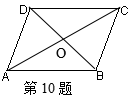
10、如图，在平行四边形ABCD中，=
，
=，则向量为______________．
（结果用和表示）
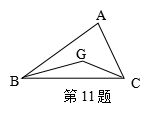
11、如图，中，G为重心，
，那样
=______________；
12、在Rt中，若
，则______________；
13、已知线段MN=2，点P是线段MN的黄金分割点，MP>NP，则MP= ______________；
14、如图：平行四边形ABCD中，E为AB中点，
，连E、F交AC于G，
则AG：GC=______________；
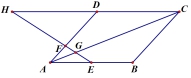
第14题
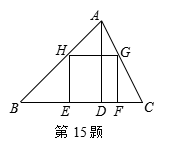
15、如图，正方形EFGH的边EF在DABC的边BC上，顶点H、G分别在边AB、AC上．假如DABC的边BC=30，高AD=20，那样正方形EFGH的边长为______________
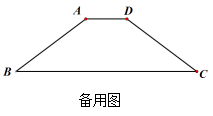
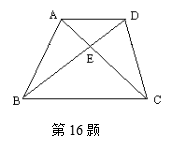
16、如图，梯形ABCD，AD//BC，AC、BD交于点E，
，则_________
17、假如把两条邻边中较短边与较长边的比值为
的矩形称作黄金矩形。现将长度为20cm的铁丝折成一个黄金矩形，这个黄金矩形较短的边长是_______________cm.
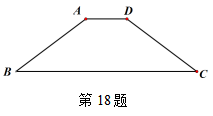
18、如图，在等腰梯形ABCD中，AD//BC,AD=2，AB=5，BC=10，点E是边BC上的一个动点（不与B,C重合），作∠AEF=∠AEB,使边EF交边CD于点F,作
,垂足为
,在中, 
，令
，-----------（1分）
则
，-（1分）又在
中，，
则
， ---（1分）于是
,即
，
解得， --（1分）∴
.----（1分）
23、（本题满分12分，第1小题6分，第2小题6分）
【解】（1）∵在中，
∴，即
，----（1分）
又在中，，∴，--（1分）
∴
，---（1分）又
，-（1分）
∴
∽.--（2分）
（2）∵是等腰直角三角形，∴
,---（1分）
又∵∽，∴，---（2分）
令,则
，---（1分）
又在中，
，（1分）∴.---（1分）
24、（本题满分12分，第1小题4分，第2小题4分，第3小题4分）
【解】（1），---（1分） ---（1分）
∠CDB=∠ABC，∠BCA=∠BCA，∴△CDB∽△CBA---（2分）
∴BC²=CD·CA，易知，BC=，AC=5，∴CD=∴---（1分）
易知∠BAC=45°，---（1分）又∵△CDB∽△CBA，∴∠BAC=∠CBD，∴∠CBD=45．---（1分）
∴△CBE为等腰直角三角形，∴可以了解E（-2，-2）．---（1分）
（3）
， （每一个2分，共4分）
25、（本题满分14分，第1小题4分，第2小题5分，第3小题5分）
【解】（1）∵AD∥BC，∴∠DAC=∠ECB．---（1分）
又∵AD=CE，AC=CB，∴△DAC≌△ECB．---（2分） ∴∠DCA＝∠EBC．---（1分）
（2）过点E作EH⊥BC，垂足为H．AE=AC–CE=
．
，∴EH=
．---（1分）
．---（1分）
∵AF//BC．∴△AEF∽△CEB，∴，---（1分）
∴，∴
．---（1分）概念域为
．---（1分）
（3）因为∠DFC=∠EBC<∠ABC, 所以∠DFC不可能为直角． （1分）
（i）当∠DGF=90°时，∠EGC=90°，由∠GCE=∠GBC，可得△GCE∽△GBC．
∴．在Rt△EHB中，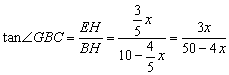 
．---（1分）
∴
，解得或．∴．---（1分）
（ii）当∠GDF=90°时，∠BCG=90°，由△GCE∽△GBC，
可得∠GEC=90°，∠CEB=90°，---（1分）
可得BE=6，CE=8，AE=2，EF=
，
．---（1分）
综上所述，假如△DFG是直角三角形，△AEF的面积为15或．
